Imagine the following situation:
- You have a big pile of money in a variety of currencies.
- You have access to currency exchanges where you can convert between currencies, but individual exchanges only convert between a subset of currencies.
- Exchanges offer a rate, this is the fraction of the target currency you obtain after exchanging a unit of the source currency. Naturally, rates are restricted to be greater than zero. Exchanges offer conversions between currencies but the rate in one direction is the reciprocal of the other direction. If A->B has a rate of R, B->A has a rate of 1/R.
- The exchanges, and their rates, are unchanging.
- Given some amount of money in one currency, you want to determine how much that amount would be worth in each possible exchangeable currency, and the conversions required to reach that amount. To make it simple for the clerks, you prefer the smallest number of currency conversions in case there are multiple ways to reach one particular currency.
Modelling as a graph
This problem is easily modelled as a graph. We can take the set of all currencies as nodes and create edges between nodes that have an exchange between them.
To model the following situation:
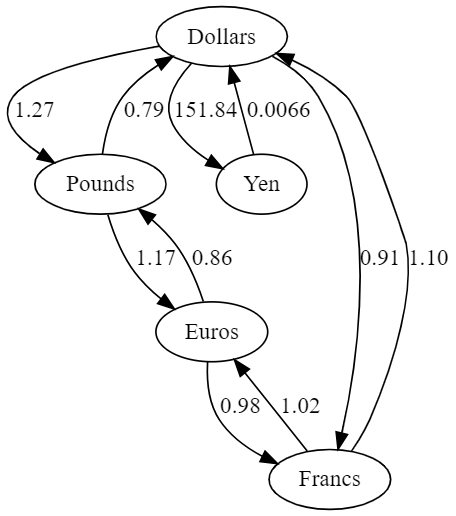
- Currencies: Pounds, Dollars, Euros, Francs, Yen
All exchange rates:
- Dollars -> Pounds, rate: 1.27
- Pounds -> Dollars, rate: 0.79
- Pounds -> Euros, rate: 1.17
- Dollars -> Yen, rate: 151.84
- Yen -> Dollars, rate: 0.0066
- Euros -> Pounds, rate: 0.86
- Euros -> Francs, rate: 0.98
- Francs -> Euros, rate: 1.02
- Dollars -> Francs, rate: 0.91
- Francs -> Dollars, rate: 1.10
(The definition of exchange rates could be simplified, defining one conversion, and using reciprocal to get the opposite conversion.)
Now, using the graph definition above, this can be drawn as
Solving the problem
Now that we have a graph representation of the problem’s parameters, we can re-state the question using our graph representation.
Note: for now, we will only consider situations where exchanges exist between all currencies, but as we will later see, this simplification will not impact our final algorithm.
- A direct conversion exists between currencies if, and only if, an edge is between the two nodes representing the source and target currency. (From our example, we can convert from pounds to dollars in one step, by exchanging 1.27 pounds for 1 dollar. This is equivalent to the edge of that weight between the two nodes).
- To convert between currencies without a direct conversions, we can take advantage of intermediate currencies. (In our example, yen can be converted to pounds by converting first to dollars, and then to pounds. That will give us 0.0066 dollars for each yen, and 1.27 pounds for each dollar. A total of 0.0066 x 1.27 = 0.0084 pounds for each yen).
- This multi-step conversion can be viewed as path in our graph, starting at the source node and ending at the destination node, with the intermediate nodes in the path being intermediate currency conversions.
From 3), we can see that when answering: “Given some amount of money in one currency, you want to determine how much that amount would be worth in each possible exchangeable currency, and the conversions required to reach that amount”, we need to know: for every node in the graph, the shortest path from the source to the destination, and the sequence of nodes in that path, and the product of all the currency converstions on the edges of that path.
In graph theory, this is an example of the “all-pairs shortest path” problem.
Algorithm
We can use a modified version of the Floyd-Warshall algorithm to solve our currency exchange problem.
Graphs are represented using an adjacency matrix of size |V|^2.
The Floyd-Warshall algorithm uses dynamic programming to solve the all-pairs shortest path problem. For each node, it compares all possible paths to determine the shortest path between a given pair. Caching allows the algorithm to complete in Θ(|V|^3) (meaning it will find all the all-pairs shortest path matrix in some positive multiple of the number of vertices cubed). The following is the pseudocode of a variant where you can reconstruct the shortest paths once the algorithm completes, modified from Wikipedia:
procedure FloydWarshallWithPathReconstruction()
let dist be a |V|x|V| array of minimum distances initialized to ∞
let prev be a |V|x|V| array of vertex indices initialized to null
for each edge (u, v) do
dist[u][v] ← 1 // we care about min distance, not the weight of the edge
prev[u][v] ← u
for each vertex v do
dist[v][v] ← 0
prev[v][v] ← v
for k from 1 to |V| do // standard Floyd-Warshall implementation
for i from 1 to |V|
for j from 1 to |V|
if dist[i][j] > dist[i][k] + dist[k][j] then
dist[i][j] ← dist[i][k] + dist[k][j]
prev[i][j] ← prev[k][j]
procedure Path(u, v)
if prev[u][v] = null then
return []
path ← [v]
while u ≠ v
v ← prev[u][v]
path.prepend(v)
return path
You can see the similarities between our defined graph format and the preprocessing required for the FloydWarshallWithPathReconstruction procedure.
This will give us a way of finding the shortest path between any two nodes. That is, the fewest conversions needed to convert between any two currencies.
However, to decrease our lookup time, it is possible to do more processing to include the multiplicative factor in the currency.
procedure GenerateConversions()
let rates be a |V|x|V| array of currency indices initialized to the conversion rate, or null if not convertible
let conversions be a |V|x|V| array of vertex indices initialized to null
for i from 1 to |V|
for j from 1 to |V|
path <- Path(i, j)
let totalRate <- 1
for edge in path: // iterate over the edges in the path
totalRate <- totalRate * rates[i][j]
conversions[i][j] = (path, totalRate)
return conversions
Analysis of GenerateConversions: the function iterates over |V| twice, and in each iteration traverses the longest path. The longest possible path for converting between currencies is |V|-1, so this procedure requires, at most, |V|^3 iterations. This is the same as the previous Floyd-Warshal step so this has no impact on the overall performance of the program.
After Θ(|V|^3) steps, we will have a table conversions, mapping source nodes to destination nodes by looking up the key dist[source][destination]. The value of this map will be a pair. The first element of the pair will be a path in the graph, this represents the conversions needed to convert between the source currency and the target currency. The second element of the pair is the overall conversion rate, this allows for converting between the two currencies with one operation.
Expanding to non-connected graphs
It is trivial to include non-connected graphs. For example, if we wanted to include sets of currencies which cannot be exchanged between groups. We can use the same algorithm, and the same setup code. We would probably expect a sparser adjacency matrix to reflect the non-connectedness of the graph. This does not alter our algorithm, as we will just be computing the all-pairs shortest path for each connected component.
Generalising
The dynamic-programming of Floyd-Warshall gives us the O(|V|^3) performance, however, if we relax our requirements, it seems we could use a general form of matrix multiplication. Given a graph, and defining a semiring of {min, +}, you can raise a distance metric to the |V|-1 power to give a matrix of all-pairs shortest path lengths. It seems like such an operation would also be applicable here. Maybe something to explore in a future blog post…